Magic Realm Combat – The Very Basics

Magic Realm Combat — The Very Basics

 

My story about my sons’ misadventures with the Tremendous Demon sparked some lively Magic Realm discussion, and ultimately, led to a friend and I playing a couple of games. My buddy enjoys Magic Realm quite a bit, but admits he rarely plays the game without me because he doesn’t quite understand combat or magic enough to play the game on his own. Even with the wonderful tool Realmspeak, he just isn’t comfortable.

That fact, and a couple of comments led me to think a few tutorial posts might be a good idea. Now, I am by no means an expert player — I die a lot. But hopefully, I will be able to add a little to your understanding of this awesome game.

The next few posts, we will be going over the combat rules, in increasing detail. If that works out, and I don’t run out of steam, or totally confuse everyone, I will move on to spell casting. So, let’s start with the basics of Magic Realm’s amazing combat system.

One thing to remember — Relax, it’s not that bad. For as legendarily complex as MR is, ultimately, the combat system deals with the same core things that any rpg combat system does. Do you hit your target? How much damage do you do? How much damage can you take? The actual guts of the combat system are pretty simple and much of the difficulty comes from making the NPCs work, and from the various additions… like horses, spell casting, etc.

The Combat Sequence

The MR combat sequence has the following steps

  • Luring
  • Random Assignment
  • Deploy
  • Actions
  • Assign Targets
  • Position Attacks and Maneuvers
  • Shift Monsters and Roll Tactics
  • Resolve Attacks
  • Wound/Fatigue
  • Check for Combat End

For this first post, we are going to focus on the core of the combat system: Do you hit your target? How much damage do you do? How much damage can you take? To do that we are going to run through a simple battle –the Captain facing a lone axe goblin.

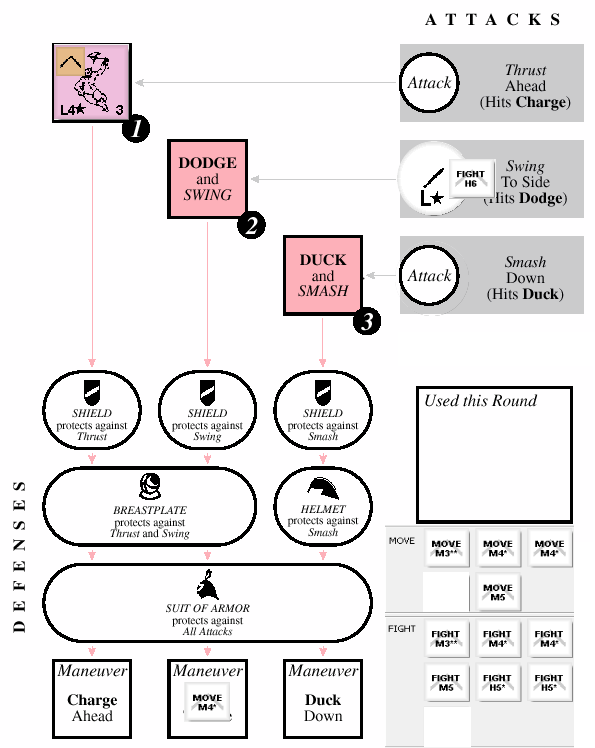
The first three phases of the combat sequence deal with which monsters attack which characters/hirelings. Because there is one unhidden character, facing a single monster, we know who is attacking whom, and so we can effectively ignore Luring, Random Assignment and Deployment for this battle. Every round, the goblin ends up on the Captain’s combat sheet, attacking him. Similarly, every round, we will be attacking the goblin.

The Captain’s 12 Combat Chits

Combat Chits — Move and Fight

Every character’s combat abilities are described by a set of 12 combat chits.

  • Chits have a Type: FIGHT chits are used to attack, MOVE chits are used to defend. (MAGIC chits also exist, but that is for another time.)
  • Chits have a Weight: Chits are either Light, Medium, Heavy orTremendous. The weight of a chit tells us what kinds of weapons and armor can be used in battle. If you have a medium weapon, you need a medium chit to use it. If you are wearing heavy armor, you can only play heavy or tremendous MOVE chits. The weight of a chit can also alter the damage of an attack. We’ll discuss that later.
  • Chits have a Speed: Chits have a speed from 1 (super fast) to 6 (really slow). The speed of the chits played in a given round can determine whether or not an attack hits, and the order in which they are resolved.
  • Chits have Effort: Each chit has anywhere from 0 to 2 effort asterisks that tell us how tiring a specific chit is to play. A chit with no asterisks does not require effort. A chit with two asterisks is very tiring to play.

So, the Captain has medium move chits, which means he can wear medium armor. His speeds are between 3-5, which is average, but notice that his MOVE M3** has two asterisks. It is very tiring to play, and we’ll usually try not to play it if possible. We have a mix of medium and heavy fight chits, and so, we can wield weapons that have a heavy weight. However, our FIGHT H chits are slow, and we start with a light weapon, so we will generally stick to the medium FIGHTs. These are similar to our MOVE chits, having speeds 3-5, but the fastest chit has two asterisks and tires us out.

Monsters Have “Chits” Too… Sort Of

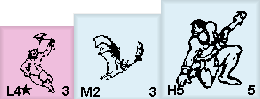
Our goblin adversary has similar “stats” as well. Denizens of the realm have two sides representing different “tactics” they use in battle. Monsters start a battle light-side up and on that side, the goblin has a block that looks like this L4*. This means that the goblins FIGHT does Light damage, and attacks with a speed of 4. Monsters don’t fatigue though… that star is a sharpness star, and it increases the damage of the goblin’s attack (we’ll talk about that later). The 3 on the opposite side of the counter without the letter, is the goblin’s MOVE speed of 3.

If the goblin “changes tactics” during combat, he will turn dark-side up. If that happens, the goblin’s attack becomes Medium (with a sharpness star), but his MOVE speed drops to 4. He hits harder, but is slower on defense.

Vulnerability

Both the Captain and the goblin have another important characteristic that isn’t shown on any counter —Vulnerability. Vulnerability is your toughness. It reflects how hard a hit you can take before you die. The Captain’s vulnerability, listed on his character card, is Medium. A medium harm hit to the Captain will kill him.

Medium, Heavy and Tremendous

The goblin’s vulnerability is also medium and we can tell this by the size of his counter. Monsters with small counters have Medium vulnerability. Monsters with the mid-sized counters are Heavy and monsters with the largest counters are Tremendous.

Weapons of War

The final thing I want to look at before getting to the actual battle is the weapon carried by the Captain. Weapons in Magic Realm have several characteristics.

  • Weapons Have a Weight: A weapon has a weight (Negligible, Light, Medium, Heavy orTremendous) that indicates how strong a FIGHT chit is required to play it. In addition, the weapon’s weight determines how much damage it does when it hits.
  • Weapons Have Sharpness: Some weapons have sharpness starts next to their weight. Just like the goblin, these stars will increase the damage done when the weapon hits. We’ll discuss exactly how much later.
  • Weapons Have a Speed: Some weapon chits have a number on them. These are speed numbers and work like FIGHT chits. 1 is really fast, 6 is really slow. If your weapon has a speed associated with it, then that number supersedes the speed on your FIGHT chit. This can be really important to remember in a fight.
  • Weapons Have an Alerted Side and an Unalerted Side: All weapon chits have two sides. The white side with no asterisk is the UNALERTED side. The red side, with the asterisk, is the ALERTED side. This is important because most weapons have totally different (better) stats when they are alerted.
  • Weapons Have a Length: Weapons have a length which, along with speed, helps determine who strikes first in a battle. The lengths of the weapons are printed in a chart in the rule book.

Now, let’s look at the Captain’s short sword — one of the crappiest weapons in the game in my opinion. The short sword is a Light weapon with one sharpness star (which as we will see, means it does Medium harm). It’s length is 3, making it one of the shortest weapons in the game, but it’s meager reach is higher than that of many of the creatures of the realm. On it’s alerted side, you can see that nothing changes. It is no better alerted than when unalerted.

Compare this to the mace, which is the weapon with which the infamous Black Knight starts the game. The mace does Medium damage, which is similar to the Light, but sharp short sword. The mace’s length is 1, which is nearly the shortest in the game. Still higher than most creatures, but the short sword has the advantage. However, we can see that, when alerted, the mace’s speed is 3, which is pretty fast. In fact, if you look at the Captain’s chits, that 3 speed is as fast as the fastest FIGHT chit, the Captain can play — his FIGHT M3**. It might not look like much now, but that is a huge advantage for the mace, and plays very heavily into the tactics used by a character that wields one.

Onward to Battle!

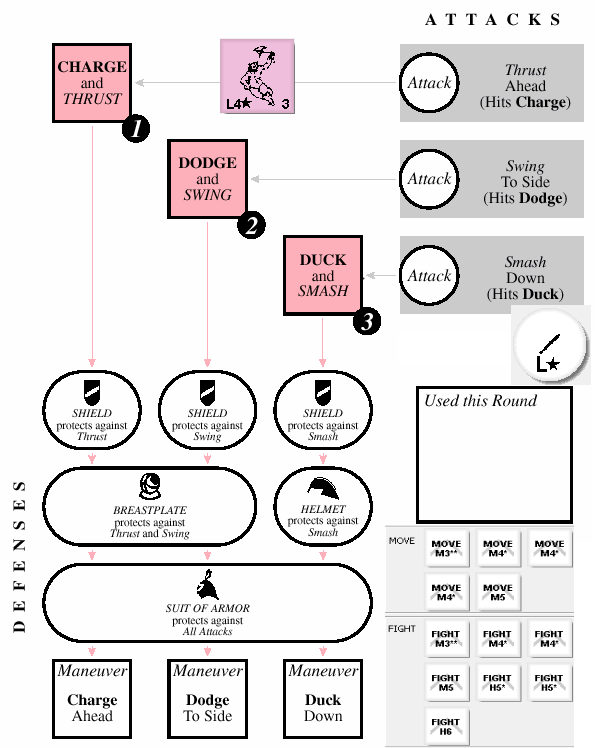
So, in a nameless clearing in the Magic Realm, a unarmored Captain faces a lone axe goblin. The Luring, Random Assignment, and Deploy steps are there to determine which denizens and NPCs attack which characters. For this first battle, we will mostly ignore those steps. The Captain isn’t hidden, and so he lures the goblin to his sheet — in other words, the goblin will be attacking the Captain every round. After I awkwardly throw all my counters on there for you to see, our sheet looks like this:

The Action Step

The action step is where we need to make our first decision. There are several things we can do on our action step, but as a fighter, the main options we need to consider are:

  • Do we run?
  • Do we alert our weapon?
Do We Run?
To run, we need to play a MOVE chit that has a speed less than the move speeds of all the enemies on our sheet. The goblin’s move is 3 and our best MOVE chit is a MOVE M3**, so we cannot run even if we wanted to. If you refer back to the goblin’s chit, you may note that its flip side has a move speed of 4 and we could flee if the goblin were to flip.
Do we even need to run? Not in this case. As we go further in the round, we will see that the Captain indeed does enough damage to kill the goblin, and that a lone goblin has no chance against our stalwart veteran.
Do We Alert?
To alert our weapon, we need to play a FIGHT chit that has a speed less than the move speeds of all the enemies on our sheet. Our fastest FIGHT is a FIGHT M3**, so we cannot alert our short sword. However, you might already realize that there is no reason to alert a short sword — it has the same characteristics either way.
So, we can’t run and we can’t alert, so we will do nothing for our action step.
The Assign Targets Step
For this step, we place our Attention chit on our target. For this battle it is pretty simple since there is only one creature to fight. However, even if we were fighting a gaggle of goblins, we would still choose a single goblin to attack — while they would all attack us each round.
The Position Step
For this step, we place the goblin in one of the three red boxes (just put him in the first box, because he might move in the Tactics step) and then place our MOVE and FIGHT chits. Our FIGHT chit, along with our weapon, goes into one of the Attack circles in the upper-right of the sheet. Our MOVE chit goes in one of theManeuver squares at the bottom of the sheet.
Placing your MOVE and FIGHT chits might seem like voodoo magic, but there are some pretty simple things to consider… (though they are not necessarily in this order):
  • Can I play a FIGHT chit to undercut the opponent’s move speed?
  • Can I play a MOVE chit to ensure I am not undercut by the opponent’s fight speed?
  • Who attacks first this round?
  • Should I cover my MOVE in case my opponent intercepts me? (What happens if my opponent hits me?)
  • Can I avoid fatigue this round?

Undercutting Your Opponent

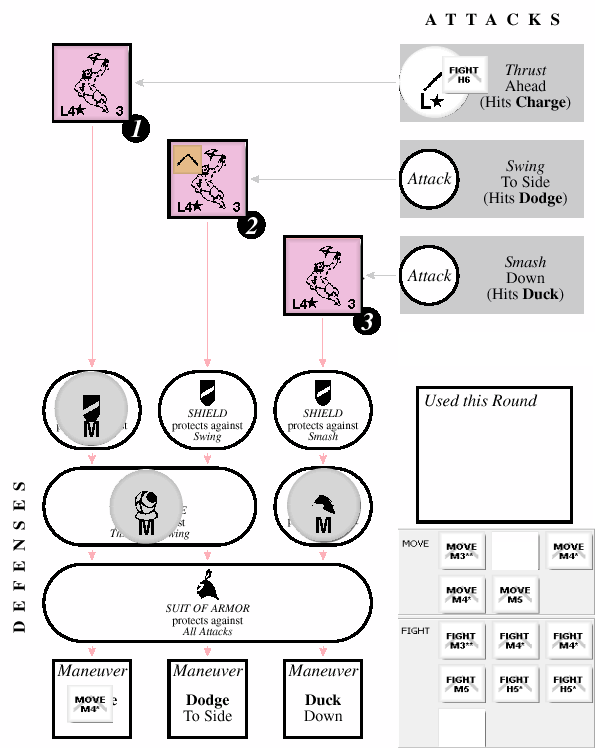
There are two ways to hit your opponent in Magic Realm. The first way it to undercut him, by playing a FIGHT chit with a speed less than his move speed. If you do this, you automatically hit your opponent that round, regardless of how he moves in the Tactics step. If we can guarantee a hit, we often should… but that depends on other considerations that come later.

For now, it is enough to note that with his move speed of 3, we cannot undercut the goblin currently, even with our best FIGHT chit (M3**). Of course, if the goblin flips during the Tactics step, we could undercut with our FIGHT M3**, but there are some other things to consider, and as you will see, there is no need to undercut the axe goblin.

Not Getting Undercut

Of course with his L4* attack, the goblin can undercut us if we don’t play a MOVE chit with a speed of 4 or better. Though it is sometimes ok to be undercut, it is often a bad thing, and in this case we want to avoid it. We will be playing one of our MOVE M4* chits to avoid being hit.

Who Attacks First?

This question is pretty important for this battle. Because it is the first round of combat, weapon length and then attack speed determines who attacks first. Our short sword has a length of 3. The axe goblin has a length of 2 (from the monster chart in the book). So, in the first round of battle, we attack first, which is a good thing.

In the second and subsequent rounds of battle, the importance is reversed. Attack speed determines who attacks first, but on attacks of equal speed, weapon length determines who has initiative. So, on later rounds, if we play a FIGHT with a speed of 5 or 6, the goblin goes first. If we play a FIGHT of 4 or better, we go first.

So… the nice thing is, because we cannot undercut the goblin, and this is the first combat round, we go first, no matter how slow our FIGHT chit is. We might as well play our slowest, heaviest, least fatiguing FIGHT chit. So, we will play our FIGHT H6… the question is where?

Intercepting Your Opponent

So far, we have determined that we are playing our MOVE M4* chit and our FIGHT H6 chit. The only question we have now is whether we will cover our move or not. This has to do with the second way to hit an enemy in Magic Realm, intercepting his maneuver. So, after you place your chits, and the Tactics step moves (and flips?) the enemies on your sheet, if your attack lines up with your target’s red box (ex. you played Thrust and he is in Thrust and Charge), you intercept and hit him. Also, if your opponent’s red box lines up with your maneuver (ex. he ends up in Duck and Smash and your maneuver is Duck), he intercepts you and hits you.

We are playing our chits to cover our move

Covering Your Move

Here’s the thing, you can’t control whether you will intercept your opponent. The red box your opponent ends up in is entirely random, so you have a 1/3 chance to intercept each round. What you can control is whether you will intercept him if he intercepts you. To do this, you play your FIGHT in the attack circle that corresponds with the maneuver in which you played your MOVE. Playing this way is called covering your move.

So, if I play my MOVE in the Charge box and my attack in the Thrust box, I have covered my move. If my targeted opponent ends up in the Thrust/Charge red box, he will intercept (and thus hit) me, but I will also intercept (and thus hit) him.

You generally want to cover your move if:

  • Your target is a dangerous opponent and
  • You will attack before your target this round and
  • You can kill your target
You want to not cover your move if:
  • Your target is dangerous and
  • You will attack after your target or
  • Your attack will not kill your target
We are going to play to cover our move. Let’s play our FIGHT H6 in the Swing attack space and let’s play our MOVE M4* in the Dodge maneuver space. Once we play our chits, it is time to move to the next step.
Shifting Monsters and Tactics
Now, we roll some dice to determine which maneuver box our opponent ends up in, and which side of his counter flips up. We roll a SINGLE die and compare it to the repositioning chart. In this case, we roll a 3 and we get “bottom right box unchanged”, meaning we switch the top two boxes. Our goblin goes to the Dodge/Swing box and whoever was in the Dodge/Swing box (no one this time) goes into Charge/Thrust.
We then roll TWO dice and if either of them is a 6, our goblin “changes tactics” and that means we flip him and use the stats on his dark side. We roll a 4 and a 2, so our goblin does not flip and our sheet ends up looking like this:
Resolve Attacks
 
Now, we can resolve our attacks — which because this is the first round of battle, we do so in order of weapon length. If you remember, our Captain’s sword is length 3, which edges out the goblins length 2 attack, so our attack is resolved before the goblin’s.
Our attack does not undercut the goblin, because our attack time of 6 is slower than the goblin’s move of 3. However, because he moved into the Swing/Dodge box, we intercept and hit the goblin regardless of our relative speeds.
Harm
Our short sword does light damage. However, it is a melee weapon and thus, the strength of our FIGHT chit matters. We played a Heavy FIGHT, which is more than the Light chit required to wield the short sword. Thisoverstrengths the weapon and increases the damage by one step. So, our Light sword now does Medium harm.
In addition, the sword has a single sharpness star. The harm done by an attack is increased by a level for each sharpness star. So, our damage is increased again from Medium to Heavy.
When our Heavy harm attack hits a Medium vulnerability goblin, the goblin is killed. Because it is killed before its attack is resolved, its attack is cancelled. This is a good thing, because as you can see, the goblin also intercepted our maneuver, which would have meant a Meduim hit (the goblin does L* damage) on the Captain… enough to kill him.
This is why we covered out move in this battle. The goblin could kill us, but could not undercut us. Thus, covering our move insured that if the goblin hit us, we would hit the goblin… knowing that our slightly longer weapon would insure we would vanquish the creature before he struck a killing blow.
Let’s Up the Ante
So, after a whole bunch of explanation, we see that the Captain can easily handle a single goblin. Let’s use what we know and see what happens to the Captain as he faces three goblins. This battle will be a tiny bit rougher, so we will give our hero his armor back… which gives us the chance to see how armor works too.
So, just like last battle, we will take all of the goblins on our sheet, and we won’t be fleeing, or alerting a weapon, so we can skip to the Position step and our sheet looks like this:
Position Step
You might be asking why we spread the goblins out into three maneuver boxes. If you understand how attacks are resolved, you realize that spreading the enemies out means that one of them is bound to intercept and hit us, so it would seem like a bad idea. Short answer… the rules make us do this. We have to fill as many boxes as we can with enemies. So three bad guys means three attacks from three different directions. We are very likely going to get hit before we can defeat all of the goblins, which is why we gave the Captain his armor.
You can see we put the armor in the armor ovals. The breastplate and the helmet have to go in the ovals in which you see them. The shield can be placed in any of the three ovals to protect any of the maneuvers. We will use it to protect our Charge. Like last fight, we played a FIGHT H6 and a MOVE M4*, and targeted the first goblin, covering our Charge maneuver with a Thrust attack. Now, we will roll some dice to reposition the monsters and see if they flip.
Our reposition die is a 5 — shift down and to the right. So, every goblin changes boxes, moving down and to the right. The guy already on the bottom gets shifted up to the Thrust/Charge box.
After Repositioning
Now we roll for each goblin to see if they flip. For the goblin in box 1, we roll a 6/2 and he flips to his dark side. The goblin in box 2 gets a 5/3 and the guy in box 3 get a 6/6, so he flips. Our sheet now looks like this:
Goblins 1&3 Change Tactics
Now, we resolve attacks. It is round one, so our length 3 short sword is first, and as you can see, we don’t undercut our target, and because he repositioned, we don’t intercept him either. We miss. The good news is that because we miss, our weapon is alerted. The bad news is, that doesn’t matter for the lame short sword.
Next, the goblin attacks are resolved. Because their weapons are the same length, and their attack times are all the same, all of their attacks happen at the same time and are resolved at the same time. For simplicity’s sake, let’s not just handle the attacks one at a time.
The goblins in boxes 2 and 3 are easy to handle. Their attack times of 4 are equal to our MOVE M4* speed, but that isn’t good enough to undercut us. Checking their attack directions, you can see that they don’t intercept our Charge move either. Both goblins 2 & 3 miss us this round… thankfully.
The goblin in box 1 on the other hand, intercepts our Charge and thus hits regardless of attack/maneuver speed. So how much harm does he do?
His attack is M4*, which is Heavy harm, which will kill the Captain… except that the Captain has his shield in the way. So, what happens when an attack hits armor?
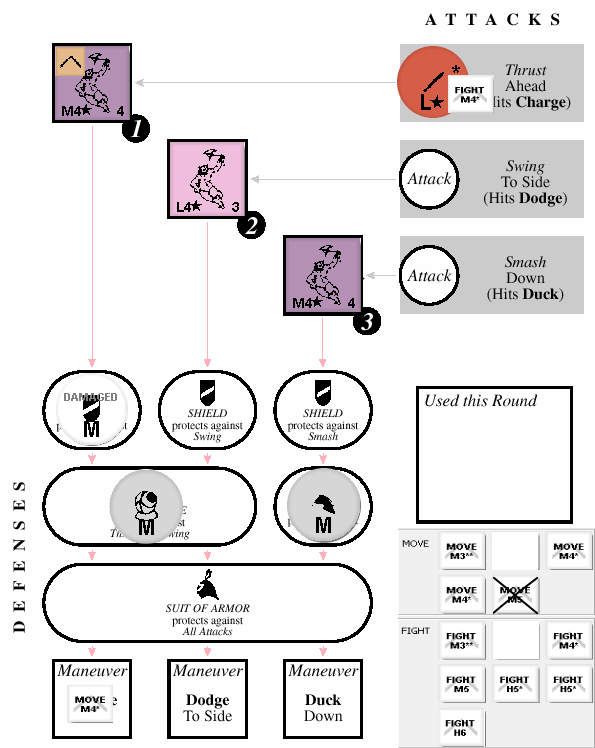
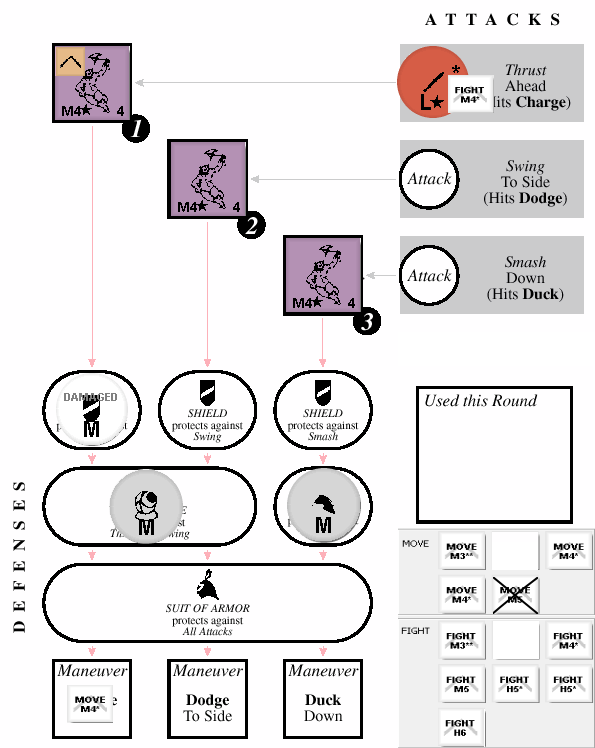
  • If the attack has sharpness stars, one of the stars is removed (if it has none, the harm is not reduced)
  • If the resulting harm exceeds the weight, the armor is destroyed
  • If the resulting harm equals the weight, the armor is damaged and flipped
  • If the resulting harm is Medium or greater, the character is wounded
Let’s resolve this Medium* attack hitting the shield.
  • First, we remove a sharpness star, making the attack a Medium harm attack
  • The Medium harm does NOT exceed the shield’s Medium weight
  • The Medium harm DOES equal the shield’s Medium weight, so the shield is flipped to the damaged side
  • The Medium attack wounds the Captain — which is great considering that without armor, that blow kills him
A wound means we take a chit out of play. If all of our chits end up wounded, or fatigued, we die, but that is a long way off. So, we choose the MOVE M5 because we are unlikely to want to play it this fight, since doing so means being undercut and hit by three angry goblins.
Fatigue
I ignored fatigue last battle because it was not going to come up. We aren’t going to fatigue this round either, but I mention it because it is bound to come up in future combat rounds.
In any given round, you are only allowed to play a total of two effort asterisks. This includes chits played to flee, to alert a weapon, and MOVE and FIGHT chits. Every chit you use is placed in the “Used this Round” box and at the end of the round, if you played two asterisks, you must fatigue one asterisk worth of chits.
Onto Round 2
 
Not a great start for the Captain. Our shield is damaged, we have a chit wounded, and still there are three goblins to deal with.
Round 2 Position Step
This is our round 2 positioning. You can see our weapon is alerted, and we are still attacking the goblin in box 1 and covering our Charge maneuver. You might also notice that we changed our FIGHT chit. We are now playing the FIGHT M4* instead of the H6. Why?
Remember that because this is round 2, attack speed determines whose attack is resolved first, followed by weapon length. We are covering our move, but if we want to kill our target before he wounds us again, we need to play an attack of at least speed 4.
Our repo die is a 4 which means no change — all the goblins stay where they are. Now, we see who flips. We roll for each goblin and only box 2 flips with a 6/3. Our sheet looks like this:
Round 2 After Repositioning/Tactics Roll
Time to resolve attacks. Every attack on the board is a speed 4, but our weapon is still longer, so we resolve first. Our attack intercepts our target in box 1, so we hit him, overstrengthing our weapon for M* harm, which kills the goblin. His attack is cancelled and just like last round, the monsters in boxes 2 & 3 neither undercut, or intercept, so they miss.
Because our attack hit, we flip our weapon to its unalerted side.
No wounds this round, but we did play two effort asterisks and so we have to fatigue a chit. Because we played both a FIGHT and a MOVE with effort, we can choose to fatigue an asterisk from either category. I choose one of my FIGHT H5* chits and it goes out of play.
Round 3
Not so bad. We have one chit fatigued and another wounded. There are two goblins on our sheet, but they are both dark side up, which gives us an option we didn’t have before. See, the dark side of the goblin counter shows a move speed of 4, which means we can play our MOVE M3** during the action step to flee the battle.
Nah… let’s ride this one out and see what happens! Like last round, we are going to play a FIGHT M4* and a MOVE M4* and cover our maneuver. We are hoping to kill a second goblin before fatigue gets to us and before the goblins wound us too much to continue.
Round 3 Position Step
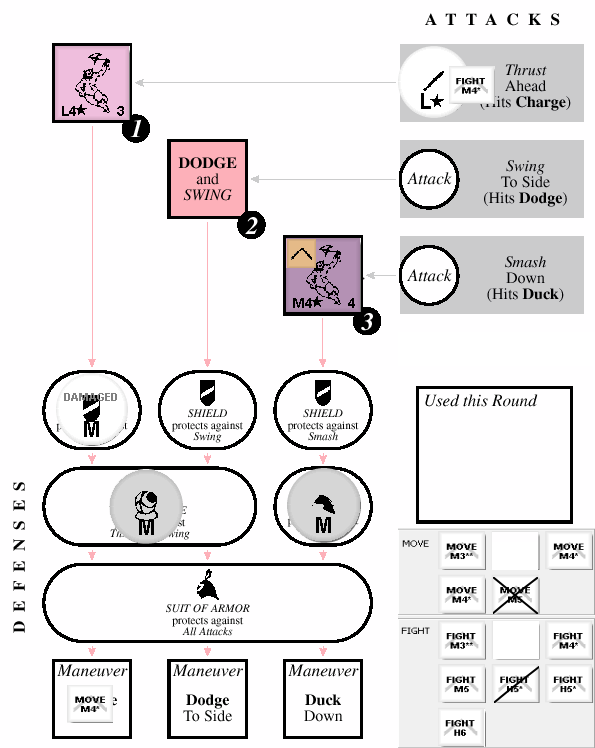Ugh, the repo roll is a 6, meaning the monsters move up and to the left. That means goblin 2 moves to box 1 and my target evades my attack by shifting to box 3. Rolling to flip, I get the goblin now in box 1 flipping with a 6/6. My sheet looks like this:
I am hit again!
We resolve first, but miss our target (who also misses me). We flip our weapon red-side up. The goblin in box 1 intercepts and hits, but we have the shield in the way. Let’s resolve the Light* attack hitting the shield.
  • First, we remove a sharpness star, making the attack a Light harm attack
  • The Light harm does NOT exceed the shield’s Medium weight
  • The Light harm does NOT equal the shield’s Medium weight and thus the shield is unaffected
  • The Light attack does NOT wound the Captain
In this case, the shield not only kept us from dying, it protected us from all harm and wasn’t even damaged! But we played two asterisks and still have to fatigue. We choose the second FIGHT H5* and go to round 4.
Round 4
For round 4, let’s change tactics a bit. We have one goblin dark-side up who has a move speed of 4. The other goblin has a move speed of 3, but if he hits armor, does no damage to us. We can undercut the dark-side goblin by playing our FIGHT M3**, and that will guarantee a hit, but what MOVE will we play in that case? We foolishly wounded our MOVE M5 previously and if we are playing a two asterisk attack, we need a no asterisk defense option.
Funny thing is, we can choose to not play a FIGHT or MOVE in a round if we don’t want to. If we fail to play a FIGHT, we don’t attack that round… not an option here. If we don’t play a MOVE, we are automatically hit by every enemy on my sheet when it comes time to resolve their attacks. That sounds dumb, but think about it.
If we play FIGHT M3** on the goblin with a move speed of 4, we will resolve first (faster attack) and hit, killing that goblin before he hits back. The other goblin will auto-hit us, but since he is currently doing L* damage, his attack will harmlessly bounce off our armor. Assuming no one flips, of course!
If the target flips, his move speed becomes 3, meaning we no longer undercut him and we might miss. If the second goblin flips, his attack becomes an M* attack, meaning he will damage our armor and wound us.
So Will They Flip?

For the “Change Tactics” roll, you roll two dice and take the highest one. The chance of one of result coming up a six (meaning either die is a six), is 11/36 or 30.6%. So, here is the breakdown of my chances:

  • 48.2%  No one flips, we kill our target and take no damage from the second. This is the best-case scenario
  • 21.2%  Our target remains dark-side, but the other guy flips. We get our kill, but the second goblin wounds us.
  • 14.1%  Our target flips to light-side, but the other guy remains. We don’t get a kill, but aren’t harmed either.
  • 7.1%  Our target flips to light-side, but the other guy remains. However, we intercept our goblin and kill him anyway.
  • 6.3%  Both goblins flip. We miss our target and are wounded by the second goblin.
  • 3.1%  Both goblins flip, but we intercept our target and kill him anyway. We are still wounded by the second goblin.
These aren’t bad odds, really. We nearly have an 80% chance of killing our target and we have almost a 70% chance of not being harmed this round. That’s pretty good. Is it better than our current tactics of playing the FIGHT and MOVE M4* and hoping for an intercept?
  • 33.3%  We intercept our target, kill him and are not hit
  • 33.3%  We don’t intercept our target and we are not intercepted
  • 23.2%  We don’t intercept our target and are intercepted by the second goblin. However, he remains light-side up and does no damage
  • 10.2%  We don’t intercept our target and are intercepted by the second goblin who flips and wounds us
We have a 33.3% chance of getting a kill if we wait for an intercept. We have nearly a 90% chance of not taking a wound. So, waiting on an intercept is a slightly more defensive tactic, but seriously drops our chance of getting a kill. Let’s go for the kill and play our FIGHT M3**!
Round 4 Position Step

Our repo roll is a 3 so the bottom right box is unchanged, meaning we flip boxes 1 & 2. We roll to change tactics and the goblin who ends up in box 1 flips with a 6/4. The goblin in box 2 does not flip.

Round 4 After Repositioning

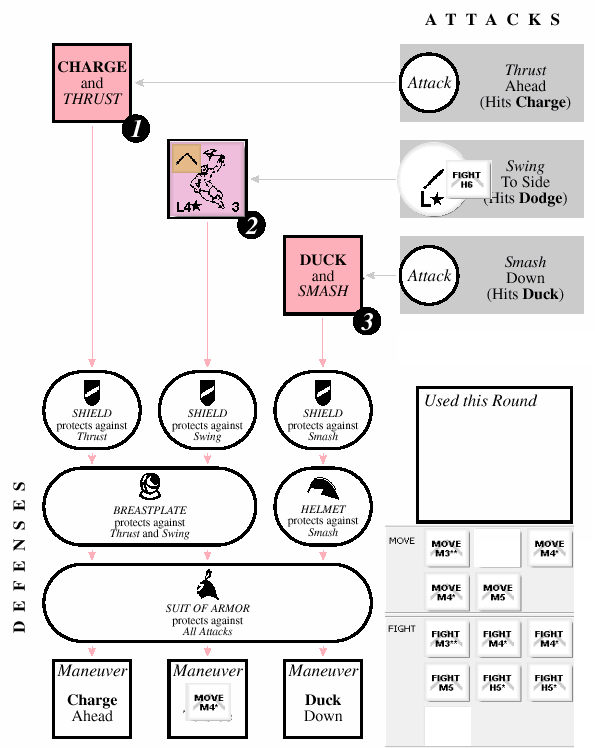
Not the worst thing that could happen, or the best. Let’s resolve attacks now. Our attack goes first because it is the fastest. Even though we don’t intercept our target, we undercut his move speed of 4 with out attack speed of 3 and so we hit, doing M* damage, and kill him. Our weapon becomes unalerted.

The goblin in box 1 “undercuts” us because we didn’t play a MOVE chit. He does M* harm, which reduces to M because it hits armor. However, that harm is enough to damage the shield again — which destroys it. The M harm also wounds us.

We played two asterisks this round, so we will have to fatigue. Because both of our asterisks were on a FIGHT chit, we have to fatigue a FIGHT. We choose one of our remaining FIGHT M4*. We also have to wound a chit. We choose one of our MOVE M4* chits.

Round 5

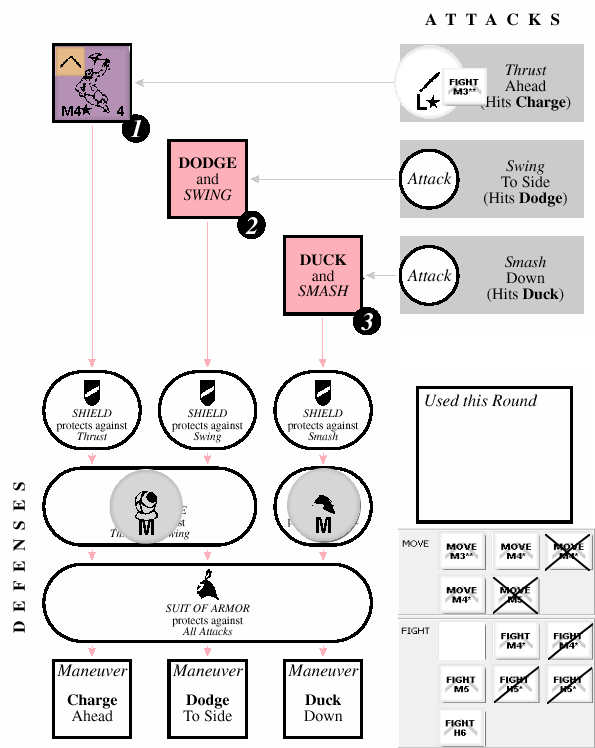Round 5 Position Step

We are down to our last goblin, and hoping for a quick end to this costly battle, I go with the FIGHT M3** again. When we roll for repositioning, we get a 2 which swaps boxes 1 & 3 and leaves the middle unchanged. More importantly, our target does not change tactics. This means that when we resolve attacks, we undercut and kill our target before he can wound us.

We have to fatigue a FIGHT again and I will fatigue the FIGHT M3**, making change by bringing our FIGHT M4* back into play. And then the combat is over. We ended up with two wounds and four asterisks fatigued. We also lost our shield. All in all a costly battle, but we felled three goblins.

We are beaten and bruised, but alive!

We will end this tutorial here. Hopefully, you have enjoyed it and learned something. We will continue this soon, adding tremendous monsters, multiple combatants and natives into the mix! If you have questions or comments, please feel free to post them.

Magic Realm Combat Part 2 — Weapon Speeds and Hiding

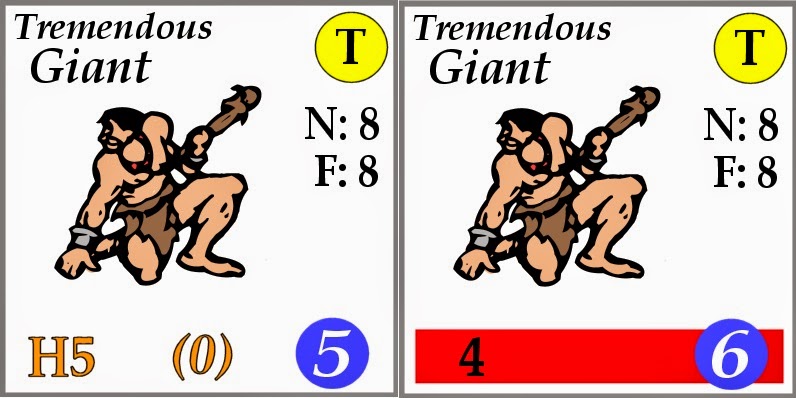
This is the first part of a larger tutorial:

Today we are going to run a couple quick battles with the White Knight. We will use the stalwart knight to focus on the concepts ofweapon speeds, alerting, and hiding as they pertain to MR’s combat system. We will also get a look at tremendous monsters and the special threat they pose.

So first, let’s set up a meeting between the powerful, but slow White Knight and a lone giant. First, let’s take a look at the White Knight and his chits.
The White Knight is a powerful fighter capable of taking down the toughest monsters in the Magic Realm. His chits are either heavy or tremendous, giving him the ability to do tremendous damage while wearing the best armor available. His main weaknesses are that he is slow, with speeds of 4-6, and that he tires easily.
In particular, notice his MOVE chits. The WK has only four of them, they are on the slow side and most have effort asterisks. Indeed, his best MOVE is a MOVE H4**, which guarantees having to fatigue a MOVE. When playing the White Knight, we need to end our fights quickly or face a slow death by wounds and fatigue!
Like the White Knight, the giant is a powerful, but ponderous combatant. His attack and move speeds are 5. He does heavy damage and has tremendous vulnerability… nothing too special so far.
However, because he is a tremendous monster, he does not have the normal light and dark sides of lesser denizens and he does not “change tactics” with a roll. Instead, whenever the giant hits us, he flips to his red side. This means that he has grabbed us. He cannot be lured from our sheet and if he hits us again, he kills instantly.
In addition, giants have a special club attack. The club is played on our sheet as though it were a second monster. We cannot attack it, but it can attack us. This means that the giant gets two shots at us each combat round. It also makes the tactic of covering our move less effective, since the giant still has a chance to hit us without getting hit by our covering attack.
We are set up for our first round of combat. Similar to our last tutorial, I am starting this battle with the WK unhidden and alone with the evil Giant. After positioning our attack and maneuver, our sheet looks like this.
Round 1 — Position Step
Notice that we are playing our MOVE H5* to keep from being undercut by the Giant’s attacks. We are also covering our move so that if his main attack hits us, we will hit him first (due to it being round 1 and our weapon is longer) and kill him. But… you might ask, why not play our FIGHT H4**, undercut the Giant’s move and kill him automatically? The reason is our great sword and its horrible unalerted side.
The great sword does H* damage, which is nice. But its unalerted side has an attack time of 6. Anytime you use a weapon, its attack time supersedes the time on your FIGHT chit. Thus, it doesn’t matter what speed FIGHT chit we play, as long as our sword is on its white side, we attack with the abysmal time of 6.
Our reposition roll is a 5, which moves every box down and to the right. Though the Giant does not roll to change tactics because he is tremendous, his club behaves like a normal creature and does roll. We roll a 2/3 and do not flip the club to it more disturbing T4 side.
Round 1 — Results
The good news is that our weapon is now alerted, allowing us to play a faster FIGHT chit. Let’s set up for round 2.
Round 2 — Position
Now, we are playing our FIGHT H4**, which will undercut the Giant, do H* harm, and kill him. The only thing we are concerned about now is that darn club. If it flips, it becomes a T4 attack with a length of 8. Our attack time is 4 and the length of the great sword is 8… the attacks will hit at the same time. That won’t kill us because of our armor, but a T attack will destroy the H armor and give us a wound — quite a price for a single giant!
Round 2 — Result
The reposition roll is a 3, which switches box 1 & 2. The club flips on a roll of 3/6 and you can see what happens. Our attack kills the Tremendous Giant, but his club hits at the exact same instant. Because the club’s T harm is higher than our H armor, it shatters the armor. Because it is medium or greater, we take a wound.
So, we lost our armor and we have to wound a chit and fatigue a FIGHT because of the FIGHT H4**, but the Giant is no more.
Hiding Changes Everything
Let’s fight the same battle with one simple difference. Let’s have the White Knight start the battle hidden. If we are hidden at the start of the battle, we have to pay a little more attention to the first part of the combat sequence.
The first step in a combat round is the Luring step. This is where we lure creatures to our combat sheet, daring them to attack us. This makes us unhidden, so we don’t lure and remain lurking in the bushes, waiting to strike.
The second step is the Random Assignment step. This step is where creatures that weren’t lured in the previous step get randomly assigned to any unhidden characters in the fight. Since we are hidden, the giant cannot be assigned to our sheet.
The Deploy step will become important in later tutorials, when we have native hirelings. For the remainder of this tutorial, we will skip deployment.
This takes us to the Action step. During the Action step, we can take one of several actions, but most of the time our main choice here is to either run away, or alert our weapon. To run, we have to play a MOVE with a speed less than that of all the creatures on our sheet. Since we are hidden, there are no creatures on our sheet, so any MOVE chit will get us out of the battle.
But, that’s not why we’re here. We are going to alert our great sword. To do that, all we need to do is play any FIGHT chit with a speed less than the move speed of all the creatures on our sheet. Since there are no creatures on our sheet, we can play a FIGHT H6 and our weapon becomes red-side up.
(Note: Any chit you use to run or alert in the Action step gets put in the “Used this Round” box and counts toward your effort limit and for fatigue. Be careful that you don’t play a tiring FIGHT chit to alert your weapon, only to not have enough effort left to not be killed later in the round.)
Now, I have alerted my great sword, cancelling its big flaw. But it gets even better once we get to the Position step!
Round 1 — Position
Because I didn’t lure the Giant, and he didn’t get assigned to me randomly, he isn’t on my sheet. In the Assignment phase, I can target him (which makes me unhidden), but he hasn’t targeted me. Attacking from a hidden position gives you one free shot against the monsters.
Round 2 — Result
So, with an alerted weapon, and no incoming club attack, I can play my FIGHT H4**, undercut the Giant and kill him automatically without the possibility of wounds or damage to my armor. Starting unhidden, the Giant has a chance to get one or two ugly shots on me. Starting hidden, the Giant is an easy kill.
The Troll and the Morning Star
For our second battle, we are going to pit the White Knight against the Tremendous Troll. The troll is a pretty scary foe for the White Knight because, although he lacks the extra club attack, he is faster than the Giant. Fast opponents are the White Knight’s bane.
In fact, if we think about what is going to happen, this is an awful combat for the White Knight. Let’s set up for round 1 and we’ll see why.
Let’s say we try to play defensively and play MOVE H4** and cover with a FIGHT H6. Our covering attack will hit the Troll before he hits us, but we can’t kill the Troll this way. The Tremendous Troll has a tremendous vulnerability and to add to that, he is also armored. (Trolls, Serpents, Vipers and Dragons are all armored.) This means that our attack will have one sharpness star removed when we calculate harm.
So, our H* attack becomes an H attack, which does nothing but annoy the Tremendous Troll. We could play a tremendous FIGHT chit, but all of our T FIGHTs have asterisks, which means we cannot play our MOVE H4**, which means the Troll undercuts us. If we don’t intercept the Troll on round 1, he undercuts us, goes red-side up and kills us on round 2.
Round 1 — Position
If we started the battle hidden, we could run, but unhidden this is pretty much our best option. We have a 1/3 chance to kill the Troll with some armor damage and a wound. Otherwise, we are ripped to shreds.
Round 1 — Result
Now the Troll is red-side up and with that attack time of 2, there is nothing we can do to save ourselves.
Round 2 — Result
Let’s take a quick look at the battle if we change the White Knight’s weapon to a morning star. The morning star is slightly shorter than the great sword (length 6) and it loses one sharpness star. At first glance, that might make it seem inferior to the sword, but it has one huge advantage. Its alerted side has an attack time of 3. That doubles our chances of winning against the mighty Tremendous Troll.
Round 1 — Position
Here we are playing our MOVE H4** and we are covering with a useless FIGHT H6. Similar to the great sword, we cannot kill the Troll with a FIGHT H, so why are we covering our move?
Well, if the Troll manages to intercept us (1/3 chance), we are dead in round 2, just like before. However, if the Troll misses us (2/3 chance), then we will miss him as well. Our weapon will then flip to its awesome speed 3 side. If we hit the Troll, our weapon does not flip, so we are covering our move to insure we miss the troll if he misses us.
Round 1 — Result (everyone missed)
So, now what? Everyone missed and we have to fatigue a MOVE, which for the White Knight is a bad thing. But, because our weapon is now a speed 3, we are guaranteed to undercut the troll.
Round 2 — Position
We play a FIGHT T5* and any MOVE. Our speed 3 attack will undercut the Troll and we will do tremendous harm and kill him. Because this is round 2, our attack speed determines the order in which the attacks are resolved, and we are fastest, so the Troll’s counterattack (which would undercut us) is negated.
Round 2 — Result

We win, because the morning star is awesome. This is why after-action reports with the White Knight often start with him trading with the Order to swap his great sword for a morning star. The alerted 3 speed is that much better than an extra sharpness star.

Still, even with a morning star, there is a 1/3 chance of dying, and a 1/3 chance of death is a little harsh. However, if you start the battle hidden, it becomes trivial if you start it hidden. Starting hidden, allows you to alert the morning star during your Action step, and devastate the Troll with a speed 3, tremendous harm attack without him even getting to target you.

Next installment, we will bring some hirelings along and see how that goes.

Magic Realm Combat 3 — Luring with Natives

This is the first part of a larger tutorial:

Quick tutorial today… we are going to battle with some natives on our side and talk about luring, deploying and battling on multiple sheets. Like last post, I am going to use RealmSpeak to manage the fight, which will make it a little easier on me… at the expense of being able to control the rolls. We’ll see how it goes.

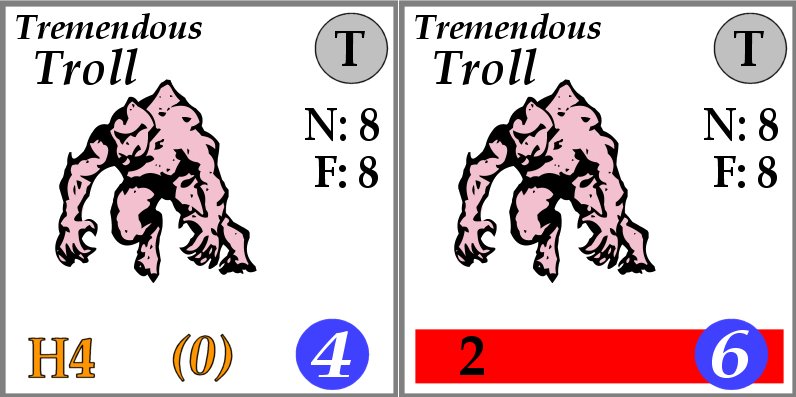
For the first battle, we are going to pit the Black Knight against two Heavy Trolls. This is a pretty good fight for the BK, though I would expect him to take a hit or two if he starts the battle unhidden. With a hireling, we should fare a little better. Let’s give the BK a rogue companion and see how we can use him.

One way we can use hirelings is to lure enemies onto their combat sheet, tricking the monsters into attacking them instead of us. Every hireling you have can lure a single enemy to his sheet each combat round. Having a native lure an enemy can save us wounds and fatigue, and to allow us to ignore our defense to play more aggressive attacks. The risk is that the native is killed in the process, which will cost us notoriety and keep us from our precious victory conditions.

The Black Knight vs. Two Heavy Trolls — Round 1

Round 1 — Luring Step

This is how we are going to use Rogue 7 in this battle — he is going to step in and take the first troll off our hands, allowing us to play an extremely aggressive attack on the second troll. To do this, R7 lures the troll in the Luring step.

Round 1 — The lured troll goes on R7’s sheet, not ours

To lure the troll, we simply place him on our hireling’s combat sheet. Notice that we flipped R7 to his dark side. When we lure an enemy onto a hireling’s sheet, we can flip him to either side. Rogue 7 has a side with a M3* attack and a 5 speed move, and another side has an L4* attack with a 4 speed move. Neither of R7’s sides has an attack that can kill a troll who is heavy and armored, so we are going to play the side with the better move speed so that R7 does not get undercut and killed.

Once R7 has lured one troll, the other is deployed to our sheet. (If there were other characters in the clearing, they might have gotten attacked by the troll in the Random Deploy step.) So, R7 has a troll, as does the Black Knight. We are still going to have to withstand an attack this round, so did the native really help at all?


He actually helped quite a bit. Because we only have a single troll to worry about, we can play a highly aggressive attack in an attempt to kill the troll before he can even attack us. The first step in this attack is to play a FIGHT chit to alert our trusty mace. Unfortunately, trolls are pretty quick and so to alert our weapon, we are going to have to burn our FIGHT M3** — using all of our effort asterisks for this round!

No need to be alarmed though. We don’t need any more effort asterisks to undercut and kill our troll. The mace is a speed 3 on its alerted side, so we can play our slowest FIGHT chit, as long as it has a Heavy strength, we will hit and do enough damage to kill the hapless troll. So, we play FIGHT H6, and a MOVE H6 and the Black Knight will kill his troll this round.

Round 1 — Position Step, our sheet

As for Rogue 7, it is just a matter of not getting hit. His move speed of 4 is fast enough to not get undercut on either of the Heavy Troll’s sides, so it really comes down to a 1/3 chance on a die roll to see if the troll intersects… in which case, the Rogue dies. So, in this case, it doesn’t matter how we play the combatants on R7’s sheet, he lives 2/3 of the time, and dies 1/3 of the time.

Round 1 — Position Step, R7’s sheet

We roll a 6 for the reposition roll, which moves the Heavy Troll from the Thrust box, into the Smash box, and he does not flip (rolled 1/5). Our hireling stays where he is and does not flip because he lured the monster onto his own sheet. When a native is battling on his own sheet, he does not roll to reposition, or to change tactics. We control where he is played and what side he is played on. Keep this in mind, because when we deploy the native to a creature’s sheet, this will change. So, R7 stays in the Charge box and the troll misses.

We have to fatigue one FIGHT asterisk because we alerted our weapon with a FIGHT M3**. We choose a FIGHT M4* because it is useless in this particular battle.

Round 2

This round is even easier than the last one. We are going to follow the same basic plan in which R7 lures the troll onto his sheet.

Round 2 — Luring the troll onto R7’s sheet

This round is better than the last one because the Black Knight has no enemies on his sheet and so he can alert his mace with any FIGHT chit he has. We pick a FIGHT M5, alert our mace, choose the troll as our target, and move onto the Position step.

Round 2 — Position Step, R7’s sheet

Since he is targeting a creature on another character’s sheet, the BK plays his position step on R7’s sheet. If you are battling other players, you still play your moves on your own sheet, keeping your plays hidden from the others, but playing solo, on RealmSpeak, we actually play our move on R7’s sheet.

Our exact positioning doesn’t matter here, because we are going to undercut the Heavy Troll and kill him with a speed 3 attack. Since this is the second round of combat, our speed 3 is certain to go before the troll, and so this is an automatic kill.

Round 2 — Results

Making good use of our hireling allowed our Black Knight to kill two heavy trolls by spending a single asterisk in fatigue. Could he have won that battle alone? Certainly, we could have even played our aggressive strategy, but it would have cost us 2 fatigued asterisks, a wound, and possibly a damaged or destroyed shield, or a damaged suit of armor… and Rogue 7 isn’t even that cool a hireling!

And to keep the concept of hiding (from the previous post in this series) fresh in your head… if the BK and R7 started the combat hidden, can you think of how you would play the battle to kill both trolls and take nofatigue or damage?

Magic Realm Combat 4 — Deploying Natives

This is the first part of a larger tutorial:

Today, we are going to go through the mechanics of deploying natives and how it differs from luring with natives. Besides horses and spell casting, deploying natives probably trips more people up than anything else in Magic Realm. Deploying natives isn’t hard, but there are a few strange bits in the rules, so we’ll go slowly and try to make everything clear.

The Maiden and the Dragon

Before we do that, let’s ponder a match up between the Woods Girl and the Tremendous Flying Dragon. The Tremendous Flying Dragon is a powerful beast, strong enough to kill even the stoutest of warriors in the realm, while still being quick enough to evade their blows. Even though the Woods Girl can undercut the dragon and can do enough damage to kill it, this battle is generally a bad idea for her. Unless she is hidden, she should run. Why?

Both giants and dragons get extra attacks. The giants have their massive clubs, and the dragons have their heads. This means that, even though it cannot undercut the Woods Girl, the Tremendous Dragon will have two chances to intercept her maneuver, doing either medium or tremendous damage — enough to kill our heroine either way.

Of course, the Woods Girl brings her formidable bow to the battle, and when it is alerted, she attacks with the incredible time of 1. This means she will undercut the dragon and harm it before it even reaches her, right? Except now, she is subject to a roll on the Missile Table. An alerted bow normally does L** damage. Because the dragon is armored, one star will come off that damage, so we are doing L*. We need to do H* harm to kill the creature, so we will need a two-level damage increase — meaning we have to roll a 1. Thankfully, because of the Woods Girl’s skill at archery, she rolls a single die on the Missile Table, so her chance of increasing her harm to the needed level is 1/6 (versus 1/36).

Those are terrible odds — our adventuress has a 1/6 chance of killing the dragon and a 5/9 chance of being killed every round.

A Hail of Arrows

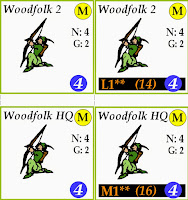
To give the Woods Girls more of a chance, we are going to have her bring her allies, the Woodfolk, to the battle. The Woodfolk is a group of three archers, two are similar in power to the Woods Girl, doing L** damage on a hit. However, the leader has a medium bow and so his damage is M**.

This changes things considerably. Instead of one chance of killing the dragon, we now have 4 shots at him. Like the Woods Girl, the native archers roll only a single die on the Missile Table, which means a roll of a 1 (or a 1 or 2 in the leader’s case) kills the dragon. Better odds than before, for certain, but to get those odds, we are going to have to learn how to deploy these natives to the battle.

Luring vs. Deploying

In our last combat tutorial post, we used a hireling to lure a troll, allowing the Black Knight to score some fairly easy kills. Deploying is very similar to luring in that it allows us to use our hirelings to attack (and be attacked by) monsters. However, the two actions are different in some pretty important ways.

Luring

  • In a given combat round, a hireling can lure a single monster
  • Conversely, a monster can only be lured by a single hireling, so you cannot make two hirelings attack the same enemy by luring
  • A lured monster is placed on the hireling’s combat sheet
  • The lured monster will attack the hireling whose sheet it is on
  • A hireling on his own combat sheet does not reposition, or change tactics — you choose what box he is in and which side he fights on, and those don’t change
  • A hireling who lures a monster instantly becomes unhidden — there is no way for a hidden hireling to attack an enemy without reprisal
Deploying
  • In a given combat round, a hireling can be deployed to a single monster
  • However, any number of hirelings can be deployed to the same monster — any number of hirelings can attack the same monster by deploying
  • Deployed natives are placed on the monster’s combat sheet
  • The monster will attack one of the hirelings deployed to his sheet — this will be the last hireling deployed to its sheet
  • A hireling on an enemy’s sheet repositions and rolls to change tactics — you cannot guarantee which maneuver is used, or which side his chit will be played on
  • A hireling who is deployed to a monster instantly becomes unhidden — there is no way for a hidden hireling to attack an enemy without reprisal
Generally, what these rules mean is that if you can manage with a one-on-one battle between each hireling and a single enemy, you should lure, because you can then control the hireling’s maneuver and whether they play light or dark side up. If you need multiple hirelings attacking a single creature, you need to deploy, but you lose the ability to control their maneuver and chit side — once you deploy your hireling, they behave randomly (just like a monster) that combat round.
The Battle
So, let’s run this battle and see what happens.
The Start of the Battle
I am not going to lure, so the monster will be “randomly” assigned to me. I will then deploy my native hirelings to the Tremendous Flying Dragon’s sheet one at a time in the order (WHQ, W2, W1). Let’s do this and see how our combat screen looks after.
Dragon’s Sheet After Deployment
A couple things happened here. First thing is, the Dragon was taken off the Wood Girl’s sheet and put on its own sheet. It is no longer going to attack the Woods Girl this round, instead it will attack the last hireling deployed to its sheet. As I deployed the Woodfolk, they went on the Dragon’s sheet and you can see the order by looking at the blue section of the image. As I deployed them, they appeared from left to right — WHQ, W2 and finally W1. Because W1 was the last hireling placed on the Dragon’s sheet, he becomes the Dragon’s target this round.

Notice we placed each archer dark-side up. This is because archer natives don’t attack at all light-side up, and we need as many attacks as possible for this tactic to work. Now, we can’t actually control if they stay dark-side up or not, but we know that the roll to change tactics is a 6 — which comes up about 30% of the time in Magic Realm. Placing our archers dark-side up to begin the round gives them a 70% chance to stay that way through the end of the round.

Next thing we will do is alert the Woods Girl’s bow with a FIGHT L4. Since she has no enemies on her sheet, any FIGHT chit will do. We then assign the Woods Girl’s target and move onto the Position phase.

Round 1 — Position Phase

It does not really matter where we position our forces this combat. Each archer will either undercut the Dragon, or not attack at all. Our attacks are all longer and faster than the Dragon’s and so we will get the first shots. We have set this combat up so that all of our attacks get a chance to kill the Dragon. However, if noneof our attacks kill the Dragon, it has a 2/3 chance of smoking poor, brave W1. All in all, we end up with a 43% chance of killing the dragon this round, a 38% chance of losing a hireling, and a 19% chance of no one dying.

Not awesome odds… but better than before.

Round 1 — Result

So what happened? Well, first let’s look at the repositioning rolls. Notice that the hirelings on the right-hand side share a single reposition roll, while the target hireling on the bottom gets his own roll. Mainly, this tells you to spread out your hirelings in the attack circles to maximize your chance to hit.

In this case, it didn’t matter because as you can see, both natives on the right rolled a 6 on their change tactics roll, so they flipped and didn’t attack at all. W1 rolled a 3 to change tactics, so he stayed dark-side up, undercutting the dragon. His missile roll was a 1, which increased his harm to H*, killing the beast!

We lucked out and won this fight without losing a single archer. Of course, there was no guarantee things would go so smoothly. The odds were barely in our favor Round 1, and if W1 died, the chances would shift in favor of the Dragon and pretty quickly spiral out of control.

I think I will end this one here. There is a little more to cover about deploying, but this has been stuck as a draft for a couple of weeks, so I want to get it out there. Keep checking back for more Magic Realm combat posts. In the near future, we will cover magic… and the even more mysterious horses!

To top